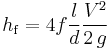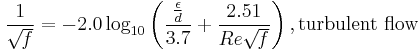Moody chart

The Moody chart or Moody diagram is a graph in non-dimensional form that relates the Darcy friction factor, Reynolds number and relative roughness for fully developed flow in a circular pipe. It can be used for working out pressure drop or flow rate down such a pipe.

Description

This dimensionless chart is used to work out pressure drop, 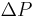\Delta P (Pa) (or head loss, 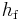h_{\mathrm{f}} (m)) and flow rate through pipes. Head loss can be calculated using the Darcy–Weisbach equation:

{h_{\mathrm{f}}=f\frac{l}{d}\frac{V^2}{2\,g}}

Not to be confused with the Fanning equation:

{h_{\mathrm{f}}=4f\frac{l}{d}\frac{V^2}{2\,g}}

which uses a friction-factor equal to one fourth the Darcy-Weisbach friction factor. Pressure drop can then be evaluated as:

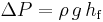\Delta P = \rho\,g\,h_{\mathrm{f}} or directly from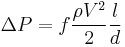 \Delta P =f \frac{\rho V^2}{2}\frac{l}{d}

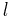Where \rho is the density of the fluid, V is the average velocity in the pipe, f is the friction factor from the Moody chart, l is the length of the pipe and d is the pipe diameter.

The basic chart plots Darcy–Weisbach friction factor against Reynolds number for a variety of relative roughnesses and flow regimes. The relative roughness being the ratio of the mean height of roughness of the pipe to the pipe diameter or 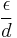\epsilon \over d .

The Moody chart can be divided into two regimes of flow: laminar and turbulent. For the laminar flow regime, the Darcy–Weisbach friction factor was determined analytically by Poiseuille and 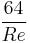\frac{64}{Re} is used. In this regime roughness has no discernible effect. For the turbulent flow regime, the relationship between the friction factor and the Reynolds number is more complex and is governed by the Colebrook equation which is implicit in f:

{1 \over \sqrt{\mathit{f}}}= -2.0 \log_{10} \left(\frac{\frac{\epsilon}{d}}{3.7} %2B {\frac{2.51}{Re \sqrt{\mathit{f} } } } \right) , \text{turbulent flow}

In 1944, Lewis Ferry Moody plotted the Darcy–Weisbach friction factor into what is now known as the Moody chart.[1]

The Fanning friction factor is 1/4 the Darcy–Weisbach one and the equation for pressure drop has a compensating factor of four.

See also

References

  1. ^ Moody, L. F. (1944), "Friction factors for pipe flow", Transactions of the ASME 66 (8): 671–684  paper on mtu.edu